Mục Lục
Công thức cấp số cộng
1. Tìm hiểu về công thức cấp số cộng:
Lịch sử của cấp số cộng liên quan đến sự phát triển của toán học qua các nền văn minh khác nhau. Công thức này đã được khám phá và sử dụng từ rất sớm, với những đóng góp quan trọng từ các nhà toán học cổ đại đến hiện đại. Dưới đây là một cái nhìn tổng quan về lịch sử phát triển của cấp số cộng:
1. Thời cổ đại
Ai Cập cổ đại: Người Ai Cập cổ đại đã sử dụng các khái niệm liên quan đến cấp số cộng trong các vấn đề liên quan đến nông nghiệp và đo đạc đất đai. Họ sử dụng các phương pháp tính toán đơn giản mà không có ký hiệu hoặc công thức rõ ràng như chúng ta biết ngày nay.
Hy Lạp cổ đại: Nhà toán học Hy Lạp Euclid (khoảng 300 TCN) đã đưa ra các định lý về cấp số cộng trong tác phẩm “Elements” (Các nguyên tố). Ông đã đề cập đến các tính chất của các dãy số và tổng của chúng trong các bài toán hình học và số học.
2. Thời kỳ Trung Cổ
Ấn Độ: Nhà toán học Ấn Độ Aryabhata (476-550 SCN) đã đóng góp nhiều cho số học và đại số, trong đó có việc nghiên cứu các dãy số và tổng của chúng. Các nhà toán học Ấn Độ khác cũng tiếp tục nghiên cứu về các dãy số trong thời kỳ này.
Hồi giáo: Nhà toán học Hồi giáo Al-Khwarizmi (780-850 SCN) cũng có những đóng góp quan trọng trong lĩnh vực số học và đại số. Các tác phẩm của ông đã ảnh hưởng lớn đến sự phát triển của toán học ở châu u sau này.
3. Thời kỳ Phục Hưng và Cận Đại
Châu u: Trong thời kỳ Phục Hưng, các nhà toán học châu u bắt đầu nghiên cứu lại các tác phẩm cổ đại và phát triển thêm các khái niệm toán học. Nhà toán học người Pháp Blaise Pascal (1623-1662) và Pierre de Fermat (1607-1665) đã nghiên cứu sâu về các dãy số và tổng của chúng, đặc biệt là trong các bài toán xác suất và số học.
4. Thời kỳ Hiện Đại
Phát triển công thức: Cấp số cộng như chúng ta biết ngày nay được phát triển và hoàn thiện trong thời kỳ hiện đại, với các ký hiệu và ngôn ngữ toán học rõ ràng. Sự phát triển của đại số và giải tích đã giúp định hình lại các khái niệm này một cách chặt chẽ và tổng quát hơn.
5. Ứng dụng trong giáo dục và khoa học
Giáo dục: Cấp số cộng được giảng dạy rộng rãi trong các chương trình giáo dục toán học trên toàn thế giới. Nó là một phần quan trọng của chương trình học từ cấp tiểu học đến đại học.
Khoa học và công nghệ: Cấp số cộng được ứng dụng trong nhiều lĩnh vực khác nhau như vật lý, kinh tế, tài chính, và kỹ thuật.
Như vậy, cấp số cộng đã có một lịch sử lâu dài và phong phú, từ thời cổ đại đến hiện đại. Sự phát triển của công thức này phản ánh sự tiến bộ của toán học qua các thời kỳ và sự ứng dụng rộng rãi của nó trong nhiều lĩnh vực.
2. Lợi ích của công thức cấp số cộng:
Cấp số cộng mang lại nhiều lợi ích và ứng dụng trong các lĩnh vực khác nhau. Dưới đây là một số lợi ích chính:
1. Giải quyết các vấn đề toán học nhanh chóng
Tìm số hạng cụ thể: Cấp số cộng cho phép tính nhanh chóng số hạng thứ
n mà không cần phải liệt kê tất cả các số hạng trước đó.
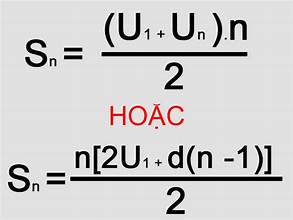
Tính tổng: Công thức tính tổng của
n số hạng đầu tiên giúp giải quyết các bài toán liên quan đến tổng dãy số một cách hiệu quả.
2. Ứng dụng trong tài chính và kinh tế
Tính lãi suất đơn: Trong một số trường hợp, lãi suất đơn có thể được tính như một cấp số cộng, giúp tính toán tổng lãi suất dễ dàng hơn.
Lập kế hoạch tài chính: Các khoản tiết kiệm hoặc đầu tư định kỳ có thể được mô hình hóa bằng cấp số cộng để dự đoán giá trị tương lai.
3. Ứng dụng trong khoa học và kỹ thuật
Phân tích dữ liệu: Cấp số cộng có thể được sử dụng để mô hình hóa các hiện tượng tự nhiên hoặc dữ liệu tăng trưởng theo một tỷ lệ cố định.
Thiết kế kỹ thuật: Trong việc bố trí các thành phần theo khoảng cách đều đặn, cấp số cộng giúp xác định vị trí chính xác của từng thành phần.
4. Hỗ trợ trong lập trình và thuật toán
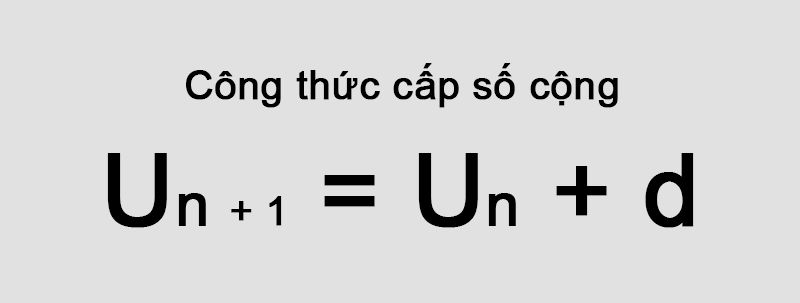
Tối ưu hóa thuật toán: Các thuật toán có thể được thiết kế hoặc tối ưu hóa bằng cách sử dụng cấp số cộng để giảm độ phức tạp tính toán.
Xử lý chuỗi số liệu: Các chương trình xử lý chuỗi số liệu sử dụng cấp số cộng để tính toán nhanh các giá trị cần thiết.
5. Ứng dụng trong đời sống hàng ngày
Quản lý thời gian: Khi lập kế hoạch công việc với khoảng cách thời gian đều đặn, cấp số cộng giúp xác định thời gian cụ thể của mỗi công việc.
Quản lý hàng hóa: Định kỳ kiểm kê hoặc nhập hàng theo chu kỳ đều đặn có thể sử dụng cấp số cộng để tính toán số lượng và thời gian cần thiết.
6. Phát triển tư duy toán học
Học tập và giảng dạy: Ccấp số cộng là một công cụ mạnh mẽ để phát triển tư duy logic và toán học, giúp học sinh hiểu rõ hơn về các khái niệm toán học cơ bản.
Những lợi ích trên cho thấy cấp số cộng không chỉ là một công cụ toán học quan trọng mà còn có nhiều ứng dụng thực tiễn trong cuộc sống và các lĩnh vực chuyên môn khác nhau.
3. Công dụng của cấp số cộng:
Cấp số cộng có nhiều công dụng quan trọng và thiết thực trong nhiều lĩnh vực khác nhau. Dưới đây là một số công dụng chính:
1. Ứng dụng trong tài chính và kinh tế
Lãi suất đơn: Giúp tính toán lãi suất đơn trong các khoản vay hoặc đầu tư.
Tiết kiệm và đầu tư định kỳ: Sử dụng để dự đoán giá trị tương lai của các khoản tiết kiệm hoặc đầu tư theo chu kỳ.
2. Ứng dụng trong khoa học và kỹ thuật
Mô hình hóa dữ liệu: Giúp mô hình hóa các hiện tượng tự nhiên hoặc dữ liệu có sự gia tăng theo tỷ lệ cố định.
Thiết kế kỹ thuật: Xác định vị trí các thành phần trong các thiết kế kỹ thuật theo khoảng cách đều đặn.
3. Lập trình và thuật toán
Tối ưu hóa thuật toán: Sử dụng cấp số cộng để giảm độ phức tạp tính toán trong các thuật toán.
Xử lý chuỗi số liệu: Giúp xử lý và tính toán các giá trị trong chuỗi số liệu một cách nhanh chóng.
4. Quản lý thời gian và công việc
Lập kế hoạch công việc: Giúp xác định thời gian cụ thể cho mỗi công việc khi lập kế hoạch với khoảng cách thời gian đều đặn.
Quản lý hàng hóa và kiểm kê: Giúp tính toán số lượng và thời gian cần thiết cho việc kiểm kê hoặc nhập hàng định kỳ.
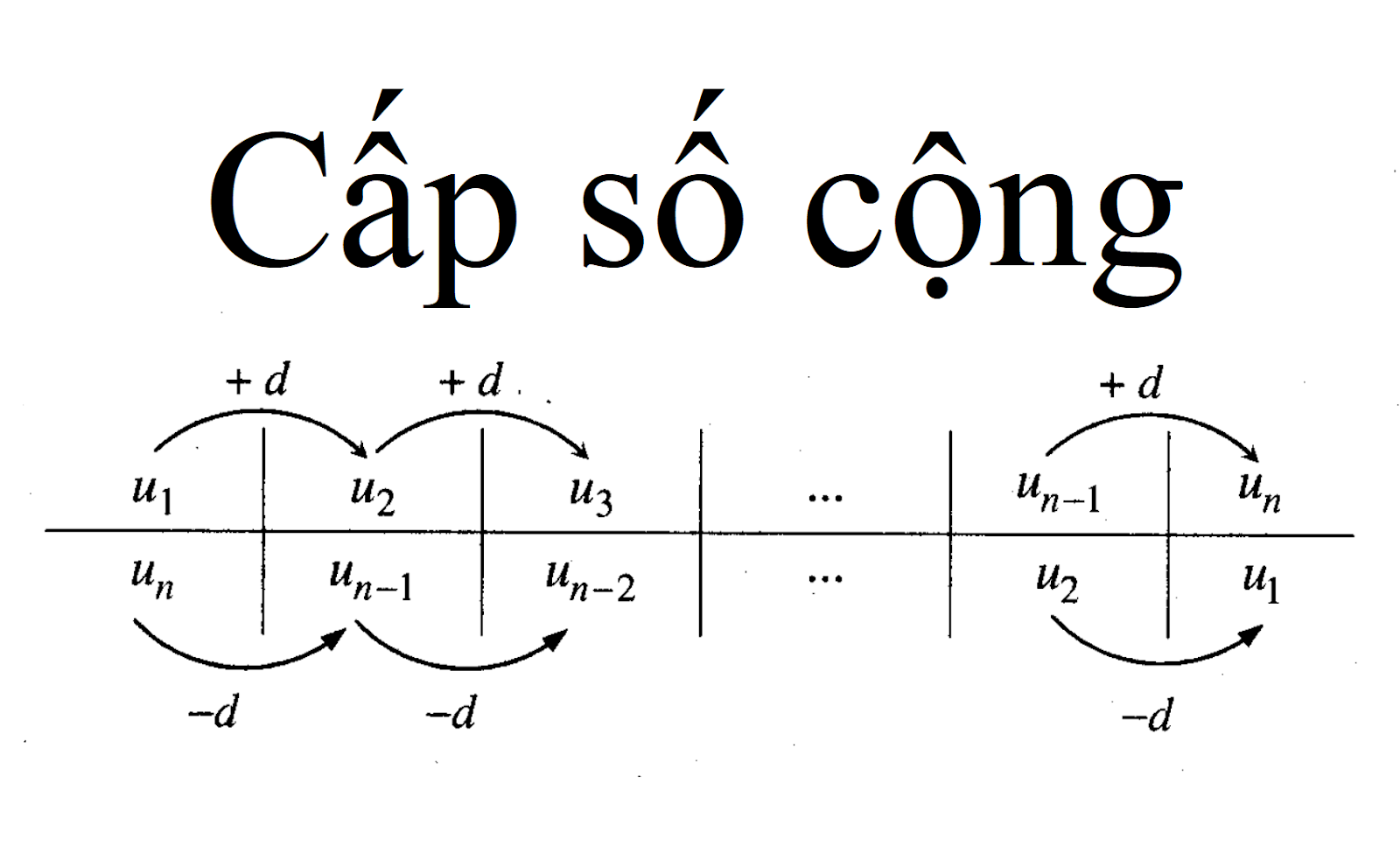
5. Giáo dục và phát triển tư duy
Giảng dạy toán học: Là công cụ giảng dạy hiệu quả để giúp học sinh hiểu rõ hơn về các khái niệm toán học cơ bản.
Phát triển tư duy logic: Giúp phát triển kỹ năng tư duy logic và phân tích.
6. Ứng dụng trong đời sống hàng ngày
Tính toán chi phí: Giúp tính toán tổng chi phí khi chi phí tăng đều theo thời gian hoặc số lượng.
Quản lý ngân sách: Sử dụng để dự toán và quản lý ngân sách cá nhân hoặc gia đình khi các khoản chi tiêu đều đặn.
Những công dụng trên cho thấy rằng cấp số cộng không chỉ là một công cụ toán học quan trọng mà còn có nhiều ứng dụng thực tế, giúp giải quyết các vấn đề trong nhiều lĩnh vực khác nhau.
4. Các ngành nghề cần áp dụng cấp số cộng:
Cấp số cộng được áp dụng rộng rãi trong nhiều ngành nghề và lĩnh vực khác nhau do tính chất đơn giản và hiệu quả của nó. Dưới đây là một số ngành nghề mà cấp số cộng thường được sử dụng:
1. Tài chính và Kế toán
Tính toán lãi suất đơn: Sử dụng để tính toán lãi suất đơn trong các khoản vay hoặc đầu tư.
Dự báo tài chính: Giúp lập kế hoạch tài chính và dự báo chi tiêu, thu nhập theo các kỳ hạn đều đặn.
2. Kinh tế học
Phân tích chuỗi thời gian: Sử dụng để phân tích dữ liệu kinh tế theo chuỗi thời gian với các khoảng thời gian đều đặn.
Mô hình hóa tăng trưởng kinh tế: Giúp mô hình hóa các mô hình tăng trưởng kinh tế theo thời gian.
3. Kỹ thuật và Công nghệ
Thiết kế kỹ thuật: Xác định vị trí các thành phần trong thiết kế kỹ thuật theo khoảng cách đều đặn.
Quản lý dự án: Sử dụng để lập lịch và quản lý thời gian các công việc trong dự án kỹ thuật.
4. Khoa học Máy tính và Lập trình
Thuật toán và cấu trúc dữ liệu: Sử dụng trong thiết kế và tối ưu hóa thuật toán, đặc biệt là các thuật toán liên quan đến dãy số và chuỗi.
Xử lý dữ liệu: Giúp xử lý và tính toán các giá trị trong chuỗi dữ liệu một cách hiệu quả.
5. Giáo dục và Nghiên cứu
Giảng dạy toán học: Là công cụ giảng dạy hiệu quả để giúp học sinh hiểu rõ hơn về các khái niệm toán học cơ bản.
Phát triển tư duy logic: Giúp phát triển kỹ năng tư duy logic và phân tích.
6. Quản lý và Điều hành
Lập kế hoạch công việc: Giúp xác định thời gian cụ thể cho mỗi công việc khi lập kế hoạch với khoảng cách thời gian đều đặn.
Quản lý hàng hóa và kiểm kê: Giúp tính toán số lượng và thời gian cần thiết cho việc kiểm kê hoặc nhập hàng định kỳ.
7. Khoa học Xã hội
Phân tích dữ liệu khảo sát: Sử dụng để phân tích dữ liệu từ các cuộc khảo sát với các khoảng thời gian hoặc mẫu điều tra đều đặn.
Nghiên cứu dân số: Giúp mô hình hóa và phân tích sự thay đổi dân số theo thời gian.
8. Y học và Sinh học
Nghiên cứu dịch tễ học: Sử dụng để phân tích sự lây lan của dịch bệnh và các hiện tượng y tế khác theo chuỗi thời gian.
Sinh học phát triển: Giúp mô hình hóa các giai đoạn phát triển của sinh vật theo thời gian.
9. Ngành Giao thông Vận tải
Quản lý lịch trình: Sử dụng để lập kế hoạch và quản lý lịch trình các chuyến xe, tàu, máy bay với các khoảng thời gian đều đặn.
Phân tích lưu lượng giao thông: Giúp phân tích và dự báo lưu lượng giao thông theo chuỗi thời gian.
Những ví dụ trên cho thấy công thức cấp số cộng không chỉ là một công cụ toán học cơ bản mà còn có ứng dụng thực tiễn rộng rãi trong nhiều ngành nghề và lĩnh vực khác nhau. Sự đơn giản và hiệu quả của nó giúp giải quyết nhiều vấn đề thực tiễn một cách dễ dàng.